“理解一切或许不重要,重要的是与世界有效交互。”
——深度学习
基本概念📚
1. 深度学习是什么🧠
深度学习是机器学习的一个子领域,其核心在于使用深层神经网络(通常包含多个隐藏层)来模拟人脑的复杂数据处理机制。通过多层次的非线性变换,深度学习能够从数据中自动提取高阶特征,无需依赖人工设计的特征。
深度学习人类历史上重要的一步,也是人工智能的核心技术、“第四次工业革命”的关键支柱。
- 🔥第一次工业革命(18世纪末):蒸汽机、机械化生产。
- 💡第二次工业革命(19世纪末):电力、流水线生产。
- 💻第三次工业革命(20世纪中后期):计算机、信息技术、自动化。
- 🤖第四次工业革命(21世纪初):人工智能、物联网、大数据、深度学习、机器人技术。
2. 深度学习有什么用❓
到今天(2025年春),深度学习领域的应用广泛。许多领域通过运用深度学习,得到了革命性的技术突破,如:图像识别、自然语言处理、语音识别、自动驾驶、推荐系统、医疗等。
3. 深度学习vs机器学习⚖️
尽管属于机器学习的一个子集,但深度学习与其他传统机器学习算法有着显著的差异:
| 维度 | 机器学习 | 深度学习 |
|---|---|---|
| 数据需求 | 小规模数据即可有效训练。 | 依赖大规模数据,性能随数据量提升。 |
| 特征工程 | 需人工设计特征(如纹理、统计量)。 | 自动学习特征,减少人为干预。 |
| 计算资源 | 通常无需高性能硬件。 | 需要GPU/TPU加速训练。 |
| 模型复杂度 | 参数少,结构简单(如线性回归)。 | 参数多,结构复杂(如百层ResNet)。 |
| 可解释性 | 模型透明,易于解释(如决策树规则)。 | 黑箱模型,解释性差。 |
| 应用场景 | 结构化数据(表格、数据库)。 | 非结构化数据(图像、文本、语音)。 |
核心组件⚙️
- 网络层:模型的基本骨架。不同神经网络层的层层叠加,是直接体现“深层神经网络”中“深层”的核心组件。不同网络层发挥不同的作用,如输入层、稠密层,CNN的卷积层,RNN的循环层,Transformer的自注意力层等等。
- 损失函数:模型的训练目标。量化评估模型预测效果与真实情况(训练数据集)的差异,如适用于分类任务的损失函数和回归损失函数
- 优化器:模型的训练方式。(主要)以梯度下降为框架的算法,用于反向传播,让模型的预测效果不断逼近损失函数定义的目标。
- 激活函数:模型的训练师。直接掌管训练模型的细节,如引入非线性、判定神经元是否激活、控制各神经元(组成神经网络层的元素)的输出,如数量、范围等等。
发展历程📜
1. 神经网络🧬
“神经网络的灵感来自生物神经元“
所谓深度学习技术,核心在于使用“深层神经网络”构建学习模型。而在“深层神经网络”出现之前,其核心技术是机器学习中“神经网络”。
- 1943年,神经生理学家Warren McCulloch和数学家Walter Pitts在《A Logical Calculus of Ideas Immanent in Nervous Activity》中提出首个神经元数学模型,将生物神经元的兴奋性和抑制性抽象为数学运算
- 1958年,心理学家Frank Rosenblatt在Cornell航空实验室发明Mark I Perceptron(感知机),首次实现权重自适应机制
神经网络发展的重要节点:
| 时间 | 模型名称 | 核心贡献 | 局限性 |
|---|---|---|---|
| 1943 | McCulloch-Pitts神经元 | 首次数学建模生物神经元 | 无学习能力,仅逻辑运算 |
| 1958 | 感知机(Perceptron) | 首次实现权重可调的学习机制 | 无法解决非线性问题(如XOR) |
| 1960 | Adaline/Madaline | 引入梯度下降和均方误差 | 仍是单层线性模型 |
感知机——首个可学习的神经网络
感知机示例(Python):
class Perceptron: def __init__(self, learning_rate=0.01, n_iters=100): self.lr = learning_rate self.n_iters = n_iters self.weights = None self.bias = None self.errors = [] def activation(self, x): return np.where(x >= 0, 1, 0) # 阶跃函数 def fit(self, X, y): n_samples, n_features = X.shape self.weights = np.zeros(n_features) self.bias = 0 for _ in range(self.n_iters): total_error = 0 for idx, x_i in enumerate(X): linear_output = np.dot(x_i, self.weights) + self.bias y_pred = self.activation(linear_output) error = y[idx] - y_pred total_error += abs(error) # 权重更新规则 self.weights += self.lr * error * x_i self.bias += self.lr * error self.errors.append(total_error) if total_error == 0: # 提前终止 break def predict(self, X): linear_output = np.dot(X, self.weights) + self.bias return self.activation(linear_output
感知机作为首个可学习的神经网络模型(首个神经网络模型是M-P神经网络模型,但不可学习),成为“机器学习”领域中的首个神经网络。
然而感知机只能解决严格的线性可分问题,无法处理非线性问题(如最简单的异或问题)
已上述感知机为例(Python):
import numpy as np import matplotlib.pyplot as plt from sklearn.datasets import make_classification from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score # 生成线性可分数据 def generate_linear_data(): X, y = make_classification( n_samples=100, n_features=2, n_classes=2, n_clusters_per_class=1, n_redundant=0, class_sep=1.5, random_state=42 ) return X, y # 生成异或数据(非线性可分) def generate_xor_data(): X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]] * 25) y = np.array([0, 1, 1, 0] * 25) return X, y # 感知机实现 class Perceptron: def __init__(self, learning_rate=0.01, n_iters=100): self.lr = learning_rate self.n_iters = n_iters self.weights = None self.bias = None self.errors = [] def activation(self, x): return np.where(x >= 0, 1, 0) # 阶跃函数 def fit(self, X, y): n_samples, n_features = X.shape self.weights = np.zeros(n_features) self.bias = 0 for _ in range(self.n_iters): total_error = 0 for idx, x_i in enumerate(X): linear_output = np.dot(x_i, self.weights) + self.bias y_pred = self.activation(linear_output) error = y[idx] - y_pred total_error += abs(error) # 权重更新规则 self.weights += self.lr * error * x_i self.bias += self.lr * error self.errors.append(total_error) if total_error == 0: # 提前终止 break def predict(self, X): linear_output = np.dot(X, self.weights) + self.bias return self.activation(linear_output) # 可视化决策边界 def plot_decision_boundary(X, y, model, title): x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1 y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1 xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01)) Z = model.predict(np.c_[xx.ravel(), yy.ravel()]) Z = Z.reshape(xx.shape) plt.contourf(xx, yy, Z, alpha=0.4) plt.scatter(X[:, 0], X[:, 1], c=y, s=20, edgecolor='k') plt.xlabel("Feature 1") plt.ylabel("Feature 2") plt.title(title) # 实验1:线性可分数据 X_linear, y_linear = generate_linear_data() X_train, X_test, y_train, y_test = train_test_split(X_linear, y_linear, test_size=0.2) perceptron = Perceptron(learning_rate=0.1, n_iters=100) perceptron.fit(X_train, y_train) predictions = perceptron.predict(X_test) plt.figure(figsize=(12, 5)) plt.subplot(1, 2, 1) plot_decision_boundary(X_linear, y_linear, perceptron, f"Linear Data (Acc: {accuracy_score(y_test, predictions):.2f})") # 实验2:异或数据 X_xor, y_xor = generate_xor_data() X_train, X_test, y_train, y_test = train_test_split(X_xor, y_xor, test_size=0.2) perceptron_xor = Perceptron(learning_rate=0.1, n_iters=1000) perceptron_xor.fit(X_train, y_train) predictions_xor = perceptron_xor.predict(X_test) plt.subplot(1, 2, 2) plot_decision_boundary(X_xor, y_xor, perceptron_xor, f"XOR Data (Acc: {accuracy_score(y_test, predictions_xor):.2f})") plt.tight_layout() plt.show()
(其中一次)运行结果:
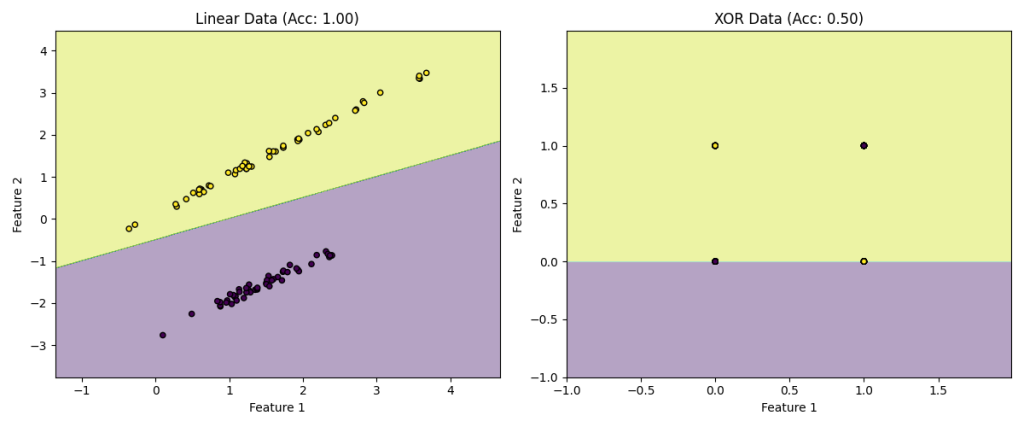
在1969年,Marvin Minsky和Seymour Papert在《Perceptrons》一书中数学证明了单层感知机无法解决异或(XOR)问题,神经网络在AI领域迎来了第一次寒冬。
3. 神经网络的寒冬❄️
神经网络乃至后来的深度学习曾度过艰难的寒冬时期:
- 第一次寒冬(1969-1985):神经网络模型(感知机)无法处理线性可分数据(xor问题)。复苏动力:激活函数引入的非线性。
- 第二次寒冬(1990-2006):反向传播算法在实际应用中暴露梯度消失(Sigmoid在深层激活函数)、过拟合(数据量不足)、计算瓶颈(训练LeNet-5需要1周)等问题。复苏动力:GPU算力推动、世界进入大数据时代、Hinton等人在2006年对深度信念网络的突破。
4. 今天的深度学习
自2012年,AlexNet在ImageNet竞赛中以压倒性的优势领先其他传统机器学习算法模型以来,深度学习高速发展,深度学习领域的论文、算法模型、应用均爆发式增长。
截止2025年春,现代深度学习模型在工业界的应用中,大多数常用模型按核心架构可分为:
- 卷积神经网络(CNN):通过卷积核提取空间局部特征,池化降维,层级抽象化。发展成熟且广泛应用。
- 循环神经网络(RNN):循环结构处理序列数据,隐藏状态传递时序信息。逐渐被Transformer替代,但在部分场景仍保持优势。
- Transformer:自注意力机制全局建模依赖关系,位置编码保留序列信息,并行计算。在不少领域逐渐取代CNN和RNN。
在复杂的任务中,也常使用混合模型(如CNN+Transformer)。


Comments NOTHING